Dynamic programming with probabilities (w/ Jane Street's April 2021 challenge)

Three months ago, I wrote an article about Jane Street’s January challenge. Continuing in the same vein, I decided to write about this month’s Jane Street problem: Bracketology 101.

There’s a certain insanity in the air this time of the year that gets us thinking about tournament brackets.  Consider a tournament with 16 competitors, seeded 1-16, and arranged in the single-elimination bracket pictured below (identical to a “region” of the NCAA Division 1 basketball tournament). Assume that when the X-seed plays the Y-seed, the X-seed has a Y/(X+Y) probability of winning. E.g. in the first round, the 5-seed has a 12/17 chance of beating the 12-seed.

Suppose the 2-seed has the chance to secretly swap two teams’ placements in the bracket before the tournament begins. So, for example, say they choose to swap the 8- and 16-seeds. Then the 8-seed would play their first game against the 1-seed and have a 1/9 chance of advancing to the next round, and the 16-seed would play their first game against the 9-seed and have a 9/25 chance of advancing.

What seeds should the 2-seed swap to maximize their (the 2-seed’s) probability of winning the tournament, and how much does the swap increase that probability? Give your answer to six significant figures.

Approach

There are \({16 \choose 2} = 120\) possible seed swaps, not that much to enumerate for a computer. The difficulty lies in the evaluation of a bracket arrangement: what is the probability that the 2-seed wins with a given bracket assignment?

A simplified example reveals the answer. Take a look at this sample arrangement with 4 seeds.

To calculate the probability that 2 wins in the second round, you have to take into account the case where 3 won the other tournament and the case where 4 won:

\[\begin{aligned} &\text{P}(\text{2 wins #2}) = \text{P}(\text{2 wins #2} \mid \text{2 wins #1}) \cdot \text{P}(\text{2 wins #1}) \\ &\text{P}(\text{2 wins #2} \mid \text{2 wins #1}) = \end{aligned} \\ \begin{aligned} &\text{P}(\text{2 wins #2} \mid \text{2 wins #1}, \text{3 wins #1}) \cdot \text{P}(\text{3 wins #1}) \\ +\; &\text{P}(\text{2 wins #2} \mid \text{2 wins #1}, \text{4 wins #1}) \cdot \text{P}(\text{4 wins #1}) \end{aligned}\]

The amount of computations scales exponentially with the amount of rounds. Worse than exponentially, actually. For the final arrangement you have take into account all other competitors of 2-seed and those competitors have to take into account their competition as well, etc. You quickly end up with a lot of recursion, and time complexity becomes nontrivial.

We can avoid this recursive mess with some careful tabulation, a technique called dynamic programming. Let’s start with a 5x16 matrix: 5 rows for the rounds (I added a dummy round #0 for simplicity), and 16 columns for the competitors. Each round we memoize the probability that the \(i\)-seed has survived so far, and we store that information in the table. And each seed starts with a probability of survival of \(1.0\):

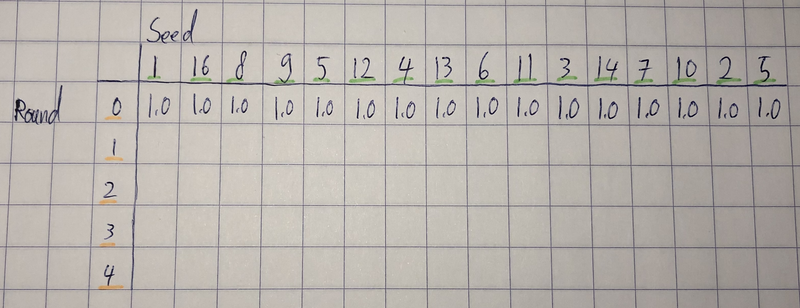
For round #1, we will start actually battling the seeds against each other. We store the probabilities of survival in the second row:

For the round #2, we will have to take into account the two different possible competitors of each participant. The probability that the 1-seed survives depends on the probabilities of survival of both the 8-seed and the 9-seed. Therefore we will group all competitors in groups of two, and carefully calculate the conditional probabilities for the next row of the table. We repeat the same for the next row in groups of four, and after that in groups of eight.

And that’s it. We can retrieve our answer in \(\text{dp}[4][\text{indexOf}(2)]\), and it only takes a computer a few milliseconds. By enumerating all 120 possible swaps we find the optimal answer: by swapping 3 and 16, we increase the probability of the 2-seed winning from \(21.6039\%\) to \(28.1619\%\).:

Further experimentation

We’ve done a single seed swap, but what happens when you repeatedly find the optimal seed swap and apply it? It turns out that if you take a random assignment of 16 seeds and repeatedly apply the greedy optimum seed swap, >99% of the time you converge an arrangement that gives the 2-seed a \(33.65\%\) chance of winning!

Most of these arrangements seem to be “equivalent” variants of the arrangement [1, 3, 4, 5, 6, 9, 8, 7, 10, 11, 12, 13, 14, 15, 16, 2] which is an arrangement that makes sense intuitively: you want to battle the 2-seed against high seeds to make it to the final round with the highest probability, and you pit all the other seeds in the other side of the bracket against each other to hopefully eliminate the 1-seed.

It’s quite surprising that greedily doing optimal swaps results in an optimal solution this often. Probably because 16 is such a low population size; I expect that this greedy algorithm becomes less effective once you start battling 256 seeds, for example.

Conclusion

You can look at my implementation here. I would like to thank Jane Street for another one of their interesting monthly challenges.